Brise
칼만필터 본문
--
--
통계적 방법으로 가우시안분포를 가지는 센서값에서 참값을 예측해내는 필터.
예측 단계[편집]
예측 단계의 계산은 무지막지하게 이루어진다.
- 연역적 상태 예측:
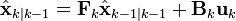
- 연역적 공분산 예측:

보정 단계[편집]
보정 단계에서는 앞단계의 예측 값과 실제 측정값간의 오차를 이용해, 이전에 얻은 값을 귀납적으로 수정한다.
- 예측 단계와 실제 측정간의 오차:
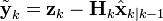
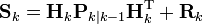
- 최적 칼만 게인(Kalman gain):
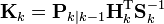
- 귀납적 상태 보정:

- 귀납적 공분산 보정:
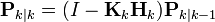
불변량[편집]
모델이 정확하고, 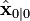 와
와 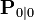 의 값이 정확하게 초기 상태 값의 몫을 반영한다면, 다음 불변량은 보존된다.
의 값이 정확하게 초기 상태 값의 몫을 반영한다면, 다음 불변량은 보존된다.
여기서 ![\textrm{E}[\xi]](http://upload.wikimedia.org/math/6/2/2/622bdf3feac7f49bbef4950f48b8fd45.png) 은
은  의 기대값이고, 공분산 매트릭스는 정확하게 추정의 공분산을 반영한다.
의 기대값이고, 공분산 매트릭스는 정확하게 추정의 공분산을 반영한다.
예제
어떤 트럭이 마찰력이 없는 x축 공간에 있다. 이 트럭은 처음에는 원점 위치에 움직이지 않고 있지만, 이후 임의의 가속도를 받으면서 움직인다. 관찰자는  시간 간격으로 트럭의 위치를 측정하지만, 이 측정값은 정확하지 않고 실제 트럭의 위치와는 어느 정도 차이가 있을 수 있다. 이 때, 관찰자는 칼만 필터를 이용해서 부정확한 측정값을 기반으로 트럭의 실제 위치를 추정할 수 있다.
시간 간격으로 트럭의 위치를 측정하지만, 이 측정값은 정확하지 않고 실제 트럭의 위치와는 어느 정도 차이가 있을 수 있다. 이 때, 관찰자는 칼만 필터를 이용해서 부정확한 측정값을 기반으로 트럭의 실제 위치를 추정할 수 있다.
우선, 트럭의 움직임에 대한 관계식 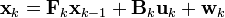 을 알맞게 이끌어내야 한다. 트럭의 상태를 나타내는 벡터
을 알맞게 이끌어내야 한다. 트럭의 상태를 나타내는 벡터 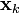 는 그 트럭의 위치와 속도로 나타내면 적당하다. 즉, 해당 벡터를 다음과 같이 정의할 수 있다.
는 그 트럭의 위치와 속도로 나타내면 적당하다. 즉, 해당 벡터를 다음과 같이 정의할 수 있다.
여기에서 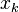 는 시점 k에서의 위치,
는 시점 k에서의 위치, 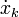 는 시점 k에서의 속도를 의미한다. 또한, 트럭에 임의로 가해지는 가속도를
는 시점 k에서의 속도를 의미한다. 또한, 트럭에 임의로 가해지는 가속도를  로 정의한다.
로 정의한다.
뉴턴의 운동 법칙에 의해, 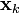 와
와  사이에는 다음과 같은 관계식이 (근사적으로) 성립한다.
사이에는 다음과 같은 관계식이 (근사적으로) 성립한다.
이것을 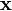 로 표현하면 다음과 같다.
로 표현하면 다음과 같다.
이 모델의 경우 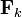 ,
, 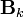 등의 값이 시간 k에 관계없이 일정하다. 이러한 상수의 경우 첨자를 생략하여 표기하였다.
등의 값이 시간 k에 관계없이 일정하다. 이러한 상수의 경우 첨자를 생략하여 표기하였다.
여기에서  가 평균이 0이고 표준편차가
가 평균이 0이고 표준편차가 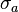 인 정규 분포를 따른다고 가정하면, 잡음 변수
인 정규 분포를 따른다고 가정하면, 잡음 변수  는 평균이 0이고 공분산이
는 평균이 0이고 공분산이
![\textbf{Q} = \textrm{cov}(\textbf{B}a) = \textrm{E}[(\textbf{B}a)(\textbf{B}a)^{\text{T}}] = \textbf{B} \textrm{E}[a^2] \textbf{B}^{\text{T}} = \textbf{B}[\sigma_a^2]\textbf{B}^{\text{T}} = \sigma_a^2 \textbf{B}\textbf{B}^{\text{T}}](http://upload.wikimedia.org/math/4/2/4/42435d1d784b9f76e9559862f7985414.png) (
(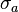 가 상수이므로 성립한다)
가 상수이므로 성립한다)
라는 것을 구할 수 있다. 이렇게 해서 트럭의 움직임에 대한 관계식을 유도했다.
그 다음에는 측정에 대한 관계식을 유도한다. 측정 잡음  가 평균이 0이고 공분산이
가 평균이 0이고 공분산이  인 정규 분포를 따른다고 가정하면,
인 정규 분포를 따른다고 가정하면,
가 얻어진다.
트럭의 초기 위치와 속도는 0이라고 가정했으므로, 초기 변수를 다음과 같이 놓을 수 있다.
만약에 트럭의 초기 상태를 알지 못한다면, 불확실성을 의미하는 공분산행렬 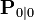 는 적당히 큰 값으로 두어야 할 필요성이 있다. 적당히 큰 수
는 적당히 큰 값으로 두어야 할 필요성이 있다. 적당히 큰 수  에 대해, 다음과 같이 초기화하면 된다.
에 대해, 다음과 같이 초기화하면 된다.
출처 : http://ko.wikipedia.org/wiki/%EC%B9%BC%EB%A7%8C_%ED%95%84%ED%84%B0
http://en.wikipedia.org/wiki/Kalman_filter
http://www.matlabinuse.com/Mastering_MATLAB/43103
http://hangondragon.blogspot.kr/2009/05/kalman-filter-part-1-linear-systems.html
http://hangondragon.blogspot.kr/2009/05/kalman-filter-part-2-kalman-filter.html
--
--
'프로그램' 카테고리의 다른 글
| 옛날 8비트 시절의 그래픽 구현 테크닉 (0) | 2015.12.20 |
|---|---|
| 정보 보안 및 해킹 관련 사이트 (0) | 2015.12.18 |
| OpenCV로 웹캠 읽어오기 (0) | 2015.12.17 |
| B-spline (0) | 2014.11.07 |
| 부동소수점 변수의 정확도 (0) | 2014.09.18 |
| 임베디드 통신 (0) | 2014.09.17 |
| 장치 대역폭 목록 (0) | 2014.09.05 |

![\textrm{E}[\textbf{x}_k - \hat{\textbf{x}}_{k|k}] = \textrm{E}[\textbf{x}_k - \hat{\textbf{x}}_{k|k-1}] = 0](http://upload.wikimedia.org/math/c/9/2/c9203d41067d91d378d6856103fedfd2.png)
![\textrm{E}[\tilde{\textbf{y}}_k] = 0](http://upload.wikimedia.org/math/b/5/a/b5a54dc85106b58adbb9909c0b3fb1a3.png)
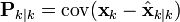
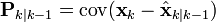




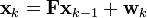


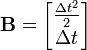


![\textbf{R} = \textrm{E}[\textbf{v}_k \textbf{v}_k^{\text{T}}] = \begin{bmatrix} \sigma_z^2 \end{bmatrix}](http://upload.wikimedia.org/math/d/3/f/d3f4efc362f41c6e1d79f2933c54eb7f.png)


